Räuber-Beute-Beziehungen – Die Volterra-Regeln

bearbeitet von Annemarie Fuckel und Annelie Wabnitz

Was versteht man unter dem Begriff „Räuber-Beute-Beziehung“?

Im Allgemeinen beschreibt diese Art Beziehung die dynamische Wechselwirkung jeweils genau einer Räuber- und genau einer Beutepopulation über einen längeren Zeitraum.

Diese Wechselwirkung lässt sich mathematisch darstellen und somit – in einem begrenzten Maß – zur Vorhersage der Entwicklung dieser Populationen genutzt werden.

Was sind die „Volterra-Regeln“?

Die Lotka-Volterra-Regeln (kurz: Volterra-Regeln) sind ein Modell zur Darstellung der quantitativen Entwicklung der Räuber- und Beutepopulation über große Zeiträume, welches drei Regeln umfasst.

Diese – beziehungsweise die ihnen zugrundeliegenden mathematischen Gleichungen – wurden in den Jahren 1925/26, unabhängig voneinander, von dem Mathematiker und Physiker VOLTERRA und dem Chemiker LOTKA formuliert.

Für die Geltung der Regeln wird vorausgesetzt, dass lediglich zwischen den betrachteten beiden Arten eine Räuber-Beute-Beziehung besteht und die sonstigen Umweltfaktoren, sowohl biotischer als auch abiotischer Art, konstant bleiben oder zu vernachlässigen sind.

Was besagen die einzelnen Regeln?

Die 1. Lotka-Volterra-Regel - Periodische Populationsschwankung

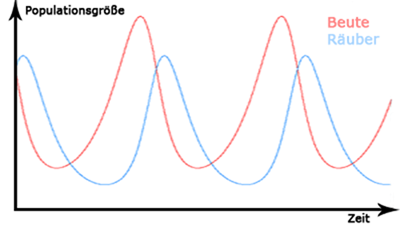
Diese Regel besagt, dass die Individuenzahlen von Räuber und Beute, bei der erfüllten Voraussetzung der konstanten Umweltfaktoren, periodisch und zeitlich versetzt schwanken.

In der nachfolgenden Grafik wird dies daraus ersichtlich, dass die Populationskurven Wellen bilden, welche zeitlich versetzte Extrema aufweisen, wobei die Kurve der Räuberpopulation (blau) diesbezüglich nachlaufend ist.

Die Begründung für diese Regel lässt sich relativ leicht erläutern: Wenn es viele Beutetiere gibt (die rote Kurve also einen hohen und noch steigenden Wert hat), kann der Nahrungsbedarf der Räuber leichter gedeckt werden und ihre Vermehrungschancen steigen, welches im Diagramm zur Folge hat, dass die blaue Kurve der Räuberpopulation beginnt zu steigen. Die Population der Räuber nimmt also zu und der Druck auf die Beutepopulation steigt, welcher sie schrumpfen lässt. Die rote Kurve hatte nun also ihr Maximum erreicht und beginnt erneut zu fallen. An einem bestimmten Punkt kommt es dann dazu, dass nicht mehr genügend Beutetiere vorhanden sind, um die Population der Räuber weiter wachsen zu lassen und sie deshalb ebenfalls wieder schrumpft. Die blaue Kurve hatte also genauso wie die rote ihr Maximum erreicht und fällt nun ebenfalls wieder. Durch den sinkenden Druck auf die Beutetiere, kann ihre Population sich langsam wieder erholen, was im Diagramm nun wieder als Steigung der roten Kurve nach einem Minimum ersichtlich wird, bis sie wieder groß genug ist, um auch die Räuberpopulation wieder wachsen zu lassen und so beginnt das Schema von Neuem.

Die 2. Lotka-Volterra-Regel - Konstanz der Mittelwerte

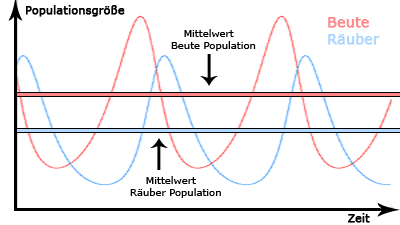
Sie sagt aus, dass bei beständigen Umweltfaktoren die durchschnittliche Größe der Population sowohl der Räuber als auch der Beute konstant bleibt, die Kurven im Diagramm sich also um einen Mittelwert bewegen. Dabei ist die Größe der anfänglichen Population nicht relevant.

Die 3. Lotka-Volterra-Regel - Störung der Mittelwerte

Diese Regel trifft Aussagen wie sich Störungen in einer Räuber-Beute-Beziehung auswirken.

Wenn sowohl Beutepopulation als auch Räuberpopulation zur gleichen Zeit um den gleichen prozentualen Anteil dezimiert werden, folgt eine kurzfristige Steigerung des Mittelwerts der Beutepopulation während der Mittelwert der Räuberpopulation sinkt. Durch den gestiegenen Mittelwert erholt sich die Beutepopulation relativ schnell wieder von der Störung, zumal die Anzahl ihrer Fressfeinde verringert ist. Die Räuberpopulation hingegen benötigt nämlich mehr Zeit zur Erholung. Dies resultiert aus der nun deutlich geringeren Individuenanzahl und wird oftmals durch die, in der Regel, längere Generationszeit noch verstärkt.

Nutzen der Regeln in der Realität

Die speziellen Voraussetzungen werden in der Natur nur selten erfüllt, denn eine Räuberart ernährt sich meistens nicht nur von genau einer Beuteart und umgekehrt haben Beutetiere in den meisten Fällen nicht nur einen Fressfeind. Außerdem sind die Umweltbedingungen in der Realität komplex und nicht beständig.

Somit lässt sich sagen, dass sich dieses Modell zwar nur schwer auf die Realität anwenden lässt, aber ihm werden in der praktischen Biologie trotzdem viel Bedeutung zu Teil, da es trotz der komplexeren Nahrungsbeziehungen und der schwankenden Umwelt durchaus noch verwertbare Vorhersagen liefert.

Quellen

Text: https://www.spektrum.de/lexikon/biologie/lotka-volterra-gleichungen/39926

https://www.frustfrei-lernen.de/biologie/raeuber-beute-beziehung.html

http://www.biologie-schule.de/lotka-volterra-regeln.php

Bilder: http://player.slideplayer.org/10/2792535/data/images/img51.jpg

http://www.biologie-schule.de/img/erste-lotka-volterra-regel.gif

http://www.biologie-schule.de/img/zweite-lotka-volterra-regel.gif

Zeitpunkt des Abrufs: 11.04.18, 13:30 Uhr